Wie fängt man einen Löwen in der Wüste?
Ein Montagnachmittag wie jeder andere. Ich habe mich mühsamst trotz
Schlafmangel zur Uni begeben und versuche krampfhaft, die Zeit zwischen
den Vorlesungen totzuschlagen. Aber die Zeit ist zäh und wehrt sich
hartnäckig. Ich raffe mich zusammen und transportiere mich zur Bibliothek,
in einem verkrampften Versuch zur produktiven gestaltung des Nachmittages.
Nach einer Zeit n, wobei n nicht besonders groß ist,
entwickeln meine Augen eine erstaunliche Entschlossenheit und fordern unnachgiebig
die Einhaltung der 126-Stunden-Woche. Die Zeit zwischen den Blinzelphasen
wird immer kürzer, irgendwie kann das Mathebuch nicht richtig motivieren.
Dann kommt mir eine Idee. Bei so vielen Büchern müßte
doch eigentlich auch ein interessantes Buch darunter sein. D.h. ein Buch,
welches man als normaler Durchschnittsstudent von sich aus in die Hand
nimmt, ja sogar aufmacht, ohne daß ein Prof einen dazu zwingt. Ich
meine, solche Bücher soll es geben, habe ich mal irgendwo aus nicht
besonders zuverlässiger Quelle gehört.
Die Vermutung erwies sich als richtig; das Buch war gut versteckt, aber
die Suche war alle Mühsale wert. Ich bin der entschiedenen Meinung,
daß man dieses herrliche Buch nicht länger der Allgemeinheit
vorenthalten sollte. Ein Buch, welches sich für den Kampf gegen die
Langeweile und Stagnation in der Mathematik einsetzt, neue Horizonte öffnet,
diese edle Wissenschaft aus dem siebten Himmel der Abstraktion herunterholt
und uns zeigt, wie wir damit Probleme des Alltags elegant meistern können,
z.B. das tägliche Problem des Löwenfangs in der Wüste. Dieser
Abschnitt beschreibt den fortschrittlichen Geist dieses Werkes so gut,
daß ich von weiteren Kommentaren absehe und die Beurteilung dem Leser
vertauensvoll übergebe.
Gefunden und abgetippt von Thorbjörn
Hansen. HTML von Ricki.
Das Einfangen von Löwen in der Wüste ist ein schönes
Beispiel anwendungsnaher Mathematik, in das sogar physikalische Aspekte
hineinspielen. Wir geben daher zum Nutzen der Leser eine Zusammenstellung
wieder, die ihm bei diesem, im täglichen Leben so häufig auftretenden
Problem, einige Leitlinien zur Lösungsfindung vermitteln.
I. Mathematische Methoden
1. Die Hilbert'sche oder axiomatische Methode
Man stellt einen Käfig in die Wüste und führt folgendes
Axiomensystem ein:
Axiom 1: Die Menge der Löwen in der Wüste ist nicht
leer.
Axiom 2: Sind Löwen in der Wüste, so ist auch ein
Löwe im Käfig.
Schlußregel: Ist p ein richtiger Satz und gilt
"wenn
p, so q", so ist auch q ein richtiger Satz.
Satz: Es ist ein Löwe im Käfig.
2. Die geometrische Methode
Man stelle einen zylindrischen Käfig in die Wüste.
1. Fall: Der Löwe ist im Käfig. Dieser Fall ist trivial.
2. Fall: Der Löwe ist außerhalb des Käfigs.
Dann stelle man sich in den Käfig und mache eine Inversion an
den Käfigwänden. Auf diese Weise gelangt der Löwe in den
Käfig un man selbst nach draußen.
Achtung: Bei Anwendung dieser Methode ist dringend darauf zu
achten, daß man sich nicht auf den Mittelpunkt des Käfigbodens
stellt, da man sonst im Unendlichen verschwindet!
3. Die Projektionsmethode
Ohne Beschränkung der Allgemeinheit nehmen wir an, daß die Wüste
eine Ebene ist. Wir projezieren sie auf eine Gerade durch den Käfig,
und die Gerade auf einen Punkt im Käfig. Damit gelangt der Löwe
in den Käfig.
4. Die Bolzano-Weierstraß-Methode
Wir halbieren die Wüste in Nord-Süd-Richtung durch einen Zaun.
Dann ist der Löwe entweder in der westlichen oder östlichen Hälfte.
Wir wollen annehmen, daß er in der westlichen Hälfte ist. Daraufhin
halbieren wir diesen westlichen Teil durch einen Zaun in Ost-West-Richtung.
Der Löwe ist entweder im nördlichen oder im südlichen Teil.
Wir nehmen an, er ist im nördlichen. Auf diese Weise fahren wir fort.
Der Durchmesser der Teile, die bei dieser Halbiererei entstehen, strebt
gegen Null. Auf diese Weise wird der Löwe schließlich von einem
Zaun beliebig kleiner Länge eingegrenzt.
5. Die mengentheoretische Methode
Die Punkte der Wüste lassen sich wohlordnen. Ausgehend vom kleinsten
Element erwischt man den Löwen durch transfinite Induktion.
Bemerkung: Diese Methode ist in Fachkreisen umstritten wegen
der Verwendung des Wohlordnungssatzes bzw. des Auswahlaxioms. Wie so oft
hat auch die vorliegende Fragestellung zu einer fruchtbaren Entwicklung
geführt. Dabei wurde schließlich eine sehr viel einfachere Methode
entdeckt, die den genannten Mangel nicht aufweist:
Man betrachte alle Teilmengen der Wüste, die den Löwen enthalten,
und bilde ihren Durchschnitt. Er enthält als einziges Element den
Löwen.
(Bei dieser Durchschneiderei ist lediglich darauf zu achten, daß
das schöne Fell des Löwen nicht zerschnitten wird!)
6. Die funktionalanalytische Methode
Die Wüste ist ein separabler Raum. Er enthält daher eine abzählbare
dichte Menge, aus der eine Folge ausgewählt werden kann, die gegen
den Löwen konvergiert. Mit einem Käfig auf dem Rücken springen
wir von Punkt zu Punkt dieser Folge und nähern uns so dem Löwen
beliebig genau.
7. Die Peano-Methode
Man konstruiere eine Peano-Kurve durch die Wüste, also eine stetige
Kurve, die durch jeden Punkt der Wüste geht. Es ist gezeigt worden,
daß man eine solche Kurve in beliebig kurzer Zeit durchlaufen kann.
Mit dem Käfig unter'm Arm durchlaufe man die Kurve in kürzerer
Zeit, als der Löwe benötigt, um sich um seine eigenen Länge
fortzubewegen.
8. Die topologische Methode
Der Löwe kann topologisch als Torus aufgefaßt werden. Man transportiere
die Wüste in den vierdimensionalen Raum. Es ist nun möglich,
die Wüste so zu deformieren, daß beim Rücktransport in
den dreidimensionalen Raum der Löwe verknotet ist. Dann ist er hilflos.
9. Die Cauchy'sche oder funktionentheoretrische Methode
Wir betrachten eine reguläre löwenwertige Funktion f auf
der Wüste. Der Käfig stehe im Punkt z der Wüste.
Man bildet dann das Integral
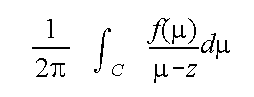
wobei C der Rand der Wüste ist. Der Wert des Integrals
ist f(z), d.h. es ist ein Löwe im Käfig.
10. Die Banach'sche oder iterative Methode
Es sei f eine Kontraktion der Wüste in sich. x0
sei ihr Fixpunkt. Auf diesen Fixpunkt stellen wir den Käfig. Durch
sukzessive Iteration
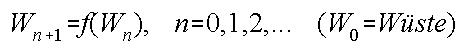
wird die Wüste auf den Fixpunkt zusammengezogen. So gelangt der
Löwe in den Käfig.
11. Die Kompaktionsmethode
Die Wüste wird ohne Beschränkung der Allgemeinheit als kompakt
vorausgesetzt. Man überdecke sie mit einer Familie von Käfigen
Ki
(i in I). Dann gibt es unter ihnen endlich viele Käfige Ki1,
... ,Kin, die bereits die ganze Wüste überdecken.
Die Durchmusterung dieser Käfige auf darin befindliche Löwen
wird als Diplomarbeit vergeben.
12. Die logische Methode oder Methode des "Tertium non datur"
Man stelle einen offenen Käfig in die Wüste und lege ein Brett
mit Leim daneben. Beides biete man dem Löwen zum Betreten an. Der
Löwe sagt dann: "Nein, auf den Leim gehe ich nicht!" Nach dem "Tertium
non datur" muß er in den Käfig gehen. Danach schlägt man
die Tür zu.
13. Die stochastische Methode
Man benötigt dazu ein Laplace-Rad, einige Würfel und eine Gauß'sche
Glocke. Mit dem Laplace-Rad fährt man in die Wüste und wirft
mit den Würfeln nach dem Löwen. Kommt er dann wutschnaubend angerannt,
so stülpt man die Gauß'sche Glocke über ihn. Unter ihr
ist er mit der Wahrscheinlichkeit eins gefangen.
14. Die didaktische Methode
Man nähere sich dem Löwen auf der Bruner'schen Spirale. Dann
elementarisiere man den Löwen zu einer Katze und fange ihn mit einer
Schale Milch.
II. Physikalische Methoden
15. Die Newton'sche Methode
Käfig und Löwe ziehen sich durch die Gravitationskraft an. Wir
vernachlässigen die Reibung. Auf diese Weise muß der Löwe
früher oder später am Käfig landen.
16. Die Heisenberg-Methode
Ort und Geschwindigkeit eines bewegten Löwen lassen sich nicht gleichzeitig
bestimmen. Da bewegte Löwen also keinen physikalisch sinnvollen Ort
in der Wüste einnehmen, kommen sie für die Jagd auch nicht in
Frage. Die Löwenjagd kann sich daher nur auf ruhende Löwen beschränken.
Das Einfangen eines ruhenden, bewegungslosen Löwen wird dem Leser
als Übungsaufgabe überlassen.
17. Die Schrödinger-Methode
Die Wahrscheinlichkeit dafür, daß sich ein Löwe zu einem
beliebigen Zeitpunkt im Käfig befindet, ist größer als
Null. Man setze sich vor den Käfig und warte.
Bemerkung: Hierbei wird üblicherweise vorausgesetzt, daß
der Käfig offen ist und man ihn zuschlagen muß, wenn der Löwe
drin ist. H. Schubert wies aber darauf hin, daß man den Käfig
wegen des Tunneleffektes auch zulassen kann. Auf diese Weise kann man bei
der elenden Warterei auch mal weggehen und ein Bierchen trinken. Aber nicht
zu lange! Denn kluge Löwen, die den Tunneleffekt begriffen haben,
verschwinden auch wieder.
18. Die Einstein'sche oder relativistische Methode
Man überfliege die Wüste nahezu mit Lichtgeschwindigkeit. Durch
die relativistische Längenkontraktion wird der Löwe flach wie
Papier. Man greife ihn, rolle ihn auf und mache ein Gummiband herum.
Bemerkung: Wir haben uns hier auf physikalische
Methoden beschränkt, die der Mathematik nahe stehen. Weitere Methoden,
insbesondere experimentalphysikalische, findet der Leser in der verdienstvollen
Abhandlung von H. Petard [1] aus dem Jahre 1938 (wie z.B. das Arbeiten
mit halbdurchlässigen Membranen, die alles außer Löwen
durchlassen. Mit ihnen siebt man die Wüste durch.) Die Sammlung von
Petard hat auch bei einigen der angegebenen mathematischen Methoden Pate
gestanden. Für einige neu aufgenommene Fangmethoden in dieser Auflage
danke ich G. Niklasch und L. Scheyde.
Auf eine schmerzliche Lücke jedoch wies H. Schubert hin, der sich
offenbar besonders tief in diese Problematik einarbeitete. Er bemerkte,
daß in all den beschriebenen Methoden die Existenz mindestens eines
Löwen vorausgesetzt wird. Wie jeder Mathematiker weiß, sind
aber Existenzprobleme häufig die haarigsten.
Schubert ist nicht der Mann, der auf halbem Wege stehen bleibt. Er teilte
mir daher die folgende Strategie mit, welche die Lücke schließt.
19. Die dialektische Methode
Man zäunt die Wüste ein, bewässert sie, sät Gras und
setzt Kaninchen aus. Die Kaninchen vermehren sich schnell. Nach Hegel kommt
daher bald der Zeitpunkt, bei dem Quantität in Qualität umschlägt,
und dann hat man einen Löwen.
All diese Methoden stammen, wie Volksmärchen,
aus dem Sagenschatz mathematischer Institute und werden auf Tagungen immer
weiter erzählt, in der Hoffnung, daß insbesondere die Jugend
sich dieses aufstrebenden Gebietes aufnehmen möchte.
Petard, H.: A Contribution to the Mathematical Theory of Big Bame Hunting.
American Math. Monthly 45, 446-447, 1938
Diese Geschmacksprobe stammt aus Friedrich Willes
Humor in
der Mathematik.
From: Martin
Müller
Zu den mathematisch-physikalischen Methoden, einen Löwen in der
Wüste mit einem Käfig zu fangen, ist in letzter Zeit in der entsprechenden
Fachliteratur überdies ein weiterer Lösungsversuch hinzugekommen,
der bei den Experten bekannt sein dürfte als
20. Das zehnte Müllersche rekursive Erreichbarkeitsproblem
Während meiner Studienzeit am Institut für Zoologische- und Jagdtechnische
Informatik in Kenia formulierte ich hierzu einen Löwen-in-der-Wüste-mit-einem-Käfig-fangen-Algorithmus
(LIFA), der in endlicher Zeit, und unter der Annahme, daß sich die
Position des Löwen und die des Käfigs durch ganze Zahlen beschreiben
läßt, dazu führt, daß der Löwe (dessen Existenz
der Einfachheit halber vorausgesetzt wird) im Käfig gefangen wird.
Die Programmverifikation überlasse ich dem geneigten Leser.
struct Ort {
int x,y;
};
struct Ort *Loewe;
struct Ort *Kaefig;
main()
{
if((Loewe->x==Kaefig->x)&&(Loewe->y==Kaefig->y)) exit(0);
else catch(Loewe,Kaefig);
}
catch(to_catch,catch_with)
struct Ort *to_catch,*catch_with;
{
if((catch_with->x==to_catch->x)&&(catch_with->y==to_catch->y))
return(0);
catch_with->x += (to_catch->x > catch_with->x)?-1:1;
catch_with->y += (to_catch->y > catch_with->y)?-1:1;
catch(to_catch,catch_with);
}
gez. Prof. Dr. hum. Maverick